জ্যামিতি কাকে বলে ? কত প্রকার ও কি কি?

Geometry ‘ শব্দটি গ্রীক Geo – ভূমি ( earth ) ও metrein – পরিমাপ ( measure ) শব্দের সমন্বয়ে তৈরি । তাই ‘ জ্যামিতি ‘ শব্দের অর্থ ‘ ভূমি পরিমাপ ‘ । যদিও ব্যুৎপত্তিগতভাবে “ জ্যামিতি ” শব্দের অর্থ ভূমির পরিমাপ তথাপি জ্যামিতি প্রকৃত পক্ষে স্থান বিষয়ক বিজ্ঞান । জ্যামিতি বা Geometry শব্দের ‘ জ্যা ’ এর অর্থ ভূমি এবং “ মিতি ’ এর অর্থ পরিমাপ ” অর্থাৎ ভূমির পরিমাপকে বলা হয় জ্যামিতি ।

বৈদিক যুগঃ
ইতিহাসের পাতা ওলটালে দেখতে পাওয়া যায় বৈদিক যুগে ভারতের আর্য মুনি – ঋষিগণ বিভিন্ন পূজার যজ্ঞের জন্য বিভিন্ন আকারের বেদি তৈরি করতেন ও আলপনা আলপনা যজ্ঞের বেদি আঁকতেন । এই সমস্ত বেদি যাতে বংশপরম্পরায় বিশুদ্ধভাবে নির্মাণ করতে পারে তার জন্য নির্মাণ পদ্ধতিকে কয়েকটি সূত্র দ্বারা বর্ণনা করা হত । এই সূত্রগুলিকে বলা হয় ’ শুল্ব সূত্র ‘ । যাঁরা এই সূত্র রচনা করেছিলেন তাঁদের বলা হয় ‘ শুল্বকার ‘ । শুল্ব কথার অর্থ দড়ি । বৈদিক যুগে রচিত এই শুল্ব সূত্র এর হাত ধরেই জ্যামিতির যাত্রা শুরু হয় । বৈদিক ঋষিগণের মধ্যে আর্যভট্ট , ব্রহ্মগুপ্ত , ভাস্করাচার্য প্রভৃতির নাম বিশেষভাবে উল্লেখযোগ্য ।

মিশরঃ
জ্যামিতিতে পূর্ণতা আনতে মিশরের ভূমিকা অপরিসীম । প্রত্যেক বছর বর্ষায় নীলনদের বন্যায় জমি জায়গার সীমানা ধুয়ে মুছে সমান হয়ে যেত । জল নামলে সেই জমির সীমানা পুনরায় নির্মাণ করার জন্য জরিপ করা হত । এই জরিপের কাজে জ্যামিতির ধারনা কাজে লাগানো হত । এ ছাড়া মিশরের পিরামিড যা আজও মিশরীয়দের উন্নত জ্যামিতি চর্চার সাক্ষ্য বহন করে ।

গ্রিসঃ
ভারতবর্ষ অথবা মিশর -এ জ্যামিতির জন্ম হলেও তা ছিল জ্যামিতির সূত্রাবলির বিক্ষিপ্ত ব্যবহার মাত্র । সূত্রাবলির মধ্যে কোনো ধারাবাহিকতা ছিল না । গ্রিসের মাটিতেই জ্যামিতি ধীরে ধীরে শৃঙ্খলাবদ্ধ হতে শুরু করে । গ্রিক গণিতজ্ঞ থ্যালেস ( Thales of Miletus ) মিশর থেকে জ্যামিতি শিখে তা গ্রিসে প্রচার করেন । তিনি জ্যামিতির মধ্যে সাংশ্লেষিক যুক্তি প্রয়োগ করেন । তিনিই প্রথম প্রমাণ করেন যে , বৃত্তের ব্যাস বৃত্তকে দুটি সমান অংশে বিভক্ত করে । তাঁর সুযোগ্য ছাত্র পিথাগোরাস ( Pythagoras of Samos ) জ্যামিতিতে নতুন মাত্রা যোগ করেন । তাঁর সমকোণী ত্রিভুজের ওপর উপপাদ্য যা পিথাগোরাসের উপপাদ্য নামে খ্যাত এবং যা আজও অপরিহার্য ।

ইউক্লিডীয় জ্যামিতিঃ
মিশরের মাটি জ্যামিতির জন্য বিখ্যাত । ভূমধ্যসাগরের তীরে মিশরের এক বিখ্যাত শহর আলেকজান্দ্রিয়াতে জন্মগ্রহণ করেন সর্বকালের অন্যতম শ্রেষ্ঠ গণিতবিদ ইউক্লিড ( Euclid ) । তিনিই প্রথম জ্যামিতির মধ্যে বিমূর্ত ধারনা এবং স্বতঃসিদ্ধ নির্ভর গণিতের প্রচলন করেন । তিনি 13 টি খণ্ডে বিভক্ত ‘ এলিমেন্টস ‘ ( Elements ) নামে একটি মূল্যবান বই লেখেন । সেই বই এর প্রথম চারটি ও ষষ্ঠ খণ্ডে জ্যামিতি নিয়ে আলোচনা করেন । তিনি 5 টি ‘ স্বীকার্য ’ ( Postulates ) এর ওপর ভিত্তি করে জ্যামিতির সমস্ত বিষয় সুনিপুণভাবে ব্যাখ্যা করেন । তাঁর প্রবর্তিত জ্যামিতিক ভাবধারাকে ‘ ইউক্লিডীয় জ্যামিতি ’ বলা হয় । জ্যামিতিশাস্ত্রে ইউক্লিডের অসামান্য অবদানের জন্য তাঁকে ‘ জ্যামিতির জনক ’ বলা হয় ।
এ ছাড়াও প্লেটো , আর্কিমিডিস , অ্যাপোলোনিয়াস প্রমুখ গণিতজ্ঞ জ্যামিতি শাস্ত্রকে সমৃদ্ধ করেন ।

জ্যামিতি কত প্রকার ও কি কি?

ব্যবহার ভেদে জ্যামিতিকে দুইভাগে ভাগ করা যায়।
যথাঃ
১.ব্যবহারিক জ্যামিতি
২.তাত্ত্বিক জ্যামিতি

ব্যবহারিক জ্যামিতি কাকে বলে?

জ্যামিতি শস্ত্রের যে শাখা পাঠ করলে বিন্দু, বস্তু, স্থান, রেখা, কোণ, ক্ষেত্র, তল প্রভৃতি অঙ্কন করার পদ্ধতি হাতে কলমে শেখা যায়তাকে ব্যবহারিক জ্যামিতি বলে।

তাত্ত্বিক জ্যামিতি কাকে বলে?

জ্যামিতি শাস্ত্রের যে শাখা পাঠ করলে জ্যামিতিক উপাত্তগুলােকে সত্য বলে প্রমাণ করা যায় এবং তা থেকে যুক্তি তর্ক ও তত্ত্বের সাহায্যে নতুন কোন সিদ্ধান্তে আসা যায় তাকে তাত্ত্বিক জ্যামিতি বলে।

জ্যামিতির প্রকারভেদঃ

এছাড়া জ্যামিতিকে আরো দুইভাগে ভাগ করা যায়। যথা-তল জ্যামিতি এবং ঘন জ্যামিতি।

তল জ্যামিতিঃ
তল জ্যামিতি দুমাত্রার। অর্থাৎ দৈর্ঘ্য ও প্রস্থ (লম্বা ও চওড়ার) বিষয়টি আলােচিত হয়ে থাকে।
তল দুই প্রকারঃসমতল ও বক্রতল।
সমতলঃযে কোন দুটি বিন্দুর সংযােজকে সরলরেখা যদি তলের উপরে অবস্থিত থাকে তাকে সমতল বলে। যেমন- চেয়ার, টেবিল, বই।
বক্রতল/অসমতলঃযে তলের পৃষ্ঠ বা উপরিভাগ সমান নয় তাকে বক্রতল বা অসমতল বলে। যেমন : মার্বেল, বল, কমলা ইত্যাদি।

ঘন জ্যামিতিঃ
ঘন জ্যামিতিতে ৩টি দিক থাকে। যথা- দৈর্ঘ্য, প্রস্থ ও উচচতা।

জ্যামিতির বিভিন্ন অংশ-ঃ
স্থানঃ
কোন বস্তু যতটুকু জায়গা দখল করে সেই জায়গাকে স্থান বলে। যেমন বাক্স, টেবিল, চেয়ার ইত্যাদি।
বস্তুঃ
যে বস্তু জায়গা দখল করে তাকেই বস্তু বলে। যেমন-বই, খাতা, টেবল। বস্তুর মাত্রা হল তিনটি। যথা-দৈর্ঘ্য, প্রস্থ, এবং উচ্চতা। বস্তুর মাত্রার উপর ভিত্তি করে বস্তুকে তিনভাগে ভাগ করা হয়েছে। যথা-একমাত্রিক, দ্বিমাত্রিক ও ত্রিমাত্রিক।
একমাত্রিকঃযে বস্তুর একটি মাত্রা আছে, তাকে বলে একমাত্রিক। যেমন : রেখা দৈর্ঘ্য।
দ্বিমাত্রিকঃযে বস্তুর দুইটি মাত্রা আছে, তাকে বলে দ্বিমাত্রিক। যেমন : তল (দৈর্ঘ্য ও প্রস্থ)
ত্রিমাত্রিকঃযে বস্তুর তিনটি মাত্রা আছে, তাকে বলে ত্রিমাত্রিক। যেমন : ঘনবস্তু। ঘনবস্তুর তিনটি মাত্রা থাকে। যথা (দৈর্ঘ্য, প্রস্থ ও উচ্চতা)।
বিন্দুঃ
দুইটি রেখা পরস্পরকে ছেদ করলে তখন বিন্দুর উপত্তি হয়। বিন্দুর শুধু অবস্থান  আছে কিন্তু কোন মাত্রা নেই। বিভিন্ন প্রকার বিন্দু এবং তার অবস্থান। যথা-
সমরেখ বিন্দুঃযেসব বিন্দু একই সরলরেখায় অবস্থান করে তাদেরকে সমরেখ বিন্দু বলে।
সমবিন্দুরেখ ঃদুই বা ততােধিক সরলরেখার একটি সাধারণ বিন্দু থাকলে তবে উক্ত রেখাগুলােকে ঐ বিন্দুর সমবিন্দুরেখ বলে।
সমতলবিন্দুঃযে সকল বিন্দু একই তলের উপর অবস্থান করে তাকে সমতলবিন্দু বলে।
শীর্ষবিন্দুঃদুটি বাহু যখন কোন একটি সাধারণ বিন্দুতে মিলিত হয় তখন তাকে শীর্ষ
বিন্দু বলে।
রেখাঃচলন্ত-বিন্দুর গতিপথকে রেখা বলে। সুতরাং বিন্দুর চলার পথকে রেখা বলে। রেখার দৈর্ঘ্য আছে, কিন্তু প্রস্থ ও উচ্চতা বা বেধ নেই।

জ্যামিতির উপাদনগুলির সংজ্ঞাঃ

জ্যামিতির মৌলিক উপাদানগুলোর সংজ্ঞাঃ
জ্যামিতির মৌলিক উপাদানগুলোর মধ্যে বিন্দু, রেখা, সমতল, কোণ, বক্ররেখা, তল (সমতল বা বক্রতল) এবং ঘনবস্তু অন্তর্ভুক্ত।

বিন্দুঃ
দুইটি রেখা পরস্পর মিলিত হলে, মিলিত স্থানে একটি বিন্দু উৎপন্ন হয়।
অর্থাৎ, পরস্পরচ্ছেদী দুইটি সরলরেখার ছেদস্থানই একটি বিন্দু। যেমন, একটি বইয়ের দুই ধার বইটির একটি কোণায় একটি বিন্দুতে মিলিত হয়।
গণিতে বিন্দুকে কেবল অবস্থান হিসাবে বিবেচনা করা হয়। অর্থাৎ বিন্দুর কেবল অবস্থান আছে বলে ধরা হয়। তাছাড়া এর কোন দৈর্ঘ্য বা প্রস্থ বা উচ্চতা বলতে কিছুই নেই। অতএব বিন্দুর মাত্রা শুণ্য।
একটি সমতলের দুইটি ভিন্ন বিন্দু দিয়ে কেবল একটি সরলরেখা আঁকা যায়।
অন্নভাবে বলা যায়, একটি সরলরেখার দৈর্ঘ্য ধীরে ধীরে কমালে সর্বশেষে সরলরেখাটি একটি বিন্দুতে পরিণত হয়।জগত হলো সকল বিন্দুর সেট।

রেখাঃ
একাধিক বিন্দু উভয়দিকে সোজাসুজি অসীম পর্যন্ত পরস্পর সংযুক্ত হয়ে যে পথ তৈরি হয়, তাই রেখা। রেখার চলার পথ সোজা (straight) বা সরল, তাই একে সরলরেখাও বলা হয়। সুতরাং বলা যায়, রেখা হলো উভয়দিকে সোজাসুজি বিন্দু চলার পথ।অন্যভাবে বলা যায়,রেখা হলো প্রস্থ বা বেধ বিহীন একটি দৈর্ঘ্য যা উভয়দিকে সোজাসুজি অসীম পর্যন্ত ক্রমবর্ধমান। রেখার কোন প্রান্ত বিন্দু নেই। এটি সবসময় অসীম পর্যন্ত ক্রমবর্ধমান।
সুতরাং একটি রেখার মধ্যে নিম্নের ধারণা দুইটি অন্তর্ভুক্তঃ১.রেখাংশ ২.রশ্মি
রশ্মিঃযার নির্দিষ্ট দৈর্ঘ্য নেই, কিন্তু প্রান্তবিন্দ আছে তাকে রশ্মি বলে।
রেখাংশঃ যার নির্দিষ্ট দৈর্ঘ্য আছে, কিন্তু ১টি প্রান্তবিন্দু আছে, তাকে রেখাংশ বলে।
রেখা সাধারণত দুই প্রকার-
১. সরলরেখা ও
২. বক্ররেখা।
সরলরেখাঃযে রেখা এক বিন্দু থেকে অন্য বিন্দুতে বা এক অবস্থান থেকে অন্য অবস্থানে পৌছতে দিক পরিবর্তন করে না তাকে সরলরেখা বলে।

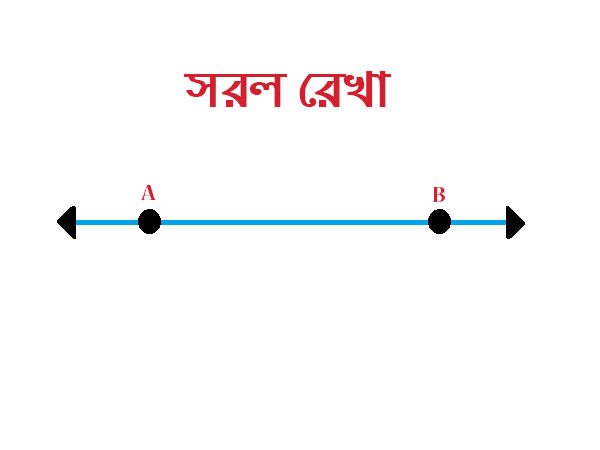
বক্ররেখাঃযে রেখা এক বিন্দু থেকে অন্য বিন্দুতে বা এক অবস্থান থেকে অন্য অবস্থানে পৌছতে দিক পরিবর্তন করে তাকে বক্ররেখা বলে।

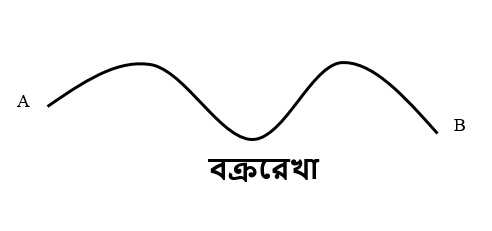
সমান্তরাল রেখাঃদুটি রেখা যদি পরস্পরের মধ্যে সর্বদা সমান দূরত্ব বজায় রেখে চলতে থাকে তবে তাকে সমান্তরাল রেখা বলে।
অতএব, এক কথায় বলতে গেলে- রেখা হলো একদম সোজা উভয়দিকে ক্রমবর্ধমান প্রান্তহীন পথবিশেষ। সুতরাং এর কেবল দৈর্ঘ্য আছে। তাই রেখা হলো একমাত্রিক জ্যামিতির অন্তর্ভুক্ত।

সমতলঃ
এক সেট রেখাকে একটার পর একটা সাজালে একটি তল উৎপন্ন হয়।
অন্নভাবে বলা যায়, সমতল হল দ্বি-মাত্রাবিশিষ্ট উঁচু নিচু নয় এমন তল (সমান তল =flat surface) যা উভয়দিকে অসীম পর্যন্ত ক্রমবর্ধমান। এর কেবল দৈর্ঘ্য ও প্রস্থ আছে। তাই সমতল দ্বিমাত্রিক জ্যামিতির অন্তর্ভুক্ত।
সুতরাং সমতলের মাত্রা দুটি হল দৈর্ঘ্য ও প্রস্থ।দৈর্ঘ্য ও প্রস্থ অবশ্যই একই সমতলে থাকবে।এটি দৈর্ঘ্য ও প্রস্থ বরাবর অসীম পর্যন্ত বিরাজমান।সকল দ্বিমাত্রিক চিত্র সমতলে অবস্থিত।

কোণঃ
দুইটি রশ্মির প্রান্তবিন্দু একই বা সাধারণ (common) হলে উৎপন্ন চিত্রকে কোণ বলে। রশ্মি দুইটিকে কোণের বাহু বলা হয়। আর সাধারণ বিন্দুটি কোণের শীর্ষ বলে পরিচিত। রশ্মি দুইটি একে অপরের সাথে কী পরিমানে আনত, তা দিয়েই কোণের পরিমাপ বুঝানো হয়।

বক্ররেখাঃ
বক্ররেখা হলো বিন্দু চলার একটি বাঁকা পথ যা কতকগুলো বিন্দু পরস্পর যুক্ত হয়ে তৈরি হয়। বক্ররেখা সোজা বা বাঁকা হতে পারে। বক্ররেখাটি যদি সোজা হয়, তাহলে এটি তখন রেখা বা সরলরেখা হয়ে যায়। তাই একটি রেখা সবসময়ই একটি বক্ররেখা। অর্থাৎ রেখা বা সরলরেখা হলো বক্ররেখার একটি বিশেষ রূপ। যেমন একটি বর্গক্ষেত্র সবসময়ই একটি আয়তক্ষেত্র। আবার বক্ররেখাটি যদি সোজা না হয়, তাহলে এটি প্রতিনিয়তই দিক পরিবর্তন করে। বক্ররেখার কেবল দৈর্ঘ্য আছে। সুতরাং বক্ররেখা একমাত্রিক জ্যামিতির অন্তর্ভুক্ত।

তলঃ
তল হলো একটি দ্বিমাত্রিক পৃষ্ঠ যা সমান (উঁচু নিচু নয় এমন) বা বক্র হতে পারে। যেমন বইয়ের একটি পৃষ্ঠা হলো একটি সমান তল বা সমতল কিন্তু বইয়ের ঐ পাতাটি দিয়ে ঝালমুড়ি ওয়ালা যখন ঝালমুড়ির ঠোঙা তৈরি করে, তখন ঠোঙার তল হয় বক্রতল। আবার বৃত্ত ক্ষেত্রের তল হলো একটি সমতল। কিন্তু গোলক এর তল হল বক্রতল। অতএব তল হলো সমতলের সাধারণ রূপ। বিপরীতক্রমে, সমতল হলো তলের একটি বিশেষ রূপ।
জগত বা ফাঁকা স্থান বা অসীম শুণ্য(Space)-
জগত বলতে বুঝায় ত্রিমাত্রিক জগত যার মাত্রা তিনটি সীমাহীনভাবে বিস্তৃত। তাই জগত বা ফাঁকা স্থান বা অসীম শুণ্য হলো সমস্ত ত্রিমাত্রিক বিন্দুর সেট। অসীম শুণ্যের মধ্যে রয়েছে যেমন অসীম ত্রিমাত্রিক বিন্দু তেমনিভাবে রয়েছে অসীম সংখ্যক তল। এক কথায় বলা যায়, অসীম শুণ্য হলো অসীম ত্রিমাত্রিক বিস্তৃতি।
অতএব, জগতে বা স্পেসে বা ফাঁকা স্থানে বা শুণ্যে সব বস্তুরই একটি আপেক্ষিক অবস্থান রয়েছে। তেমনিভাবে সেখানে সব বস্তুরই একটি আপেক্ষিক দিকও রয়েছে।
ত্রিমাত্রিক জগতে যেকোনো বস্তুকেই বলা হয় ঘনবস্তু।

ইউক্লিডিও জ্যামিতিঃ
ইউক্লিড তার তের খণ্ডের “Elements” গ্রন্থের প্রথম খণ্ডের শুরুতেই জ্যামিতির মৌলিক বিষয় বিন্দু, রেখা এবং তলের সংজ্ঞা দিয়েছেন। যদিও আধুনিক গণিতে এসব সংজ্ঞা স্থান বিশেষে কিছুটা অসম্পূর্ণ, তবুও এগুলোই জ্যামিতির মূল ভিত্তি।
ইউক্লিডিও সংজ্ঞা-
ইউক্লিড প্রদত্ত সংজ্ঞাসমূহ নিম্নরূপঃ
১.যার কোন অংশ নাই, তাই বিন্দু।
২.রেখার কোনো প্রান্ত বিন্দু নেই।
৩.যার কেবল দৈর্ঘ্য আছে, কিন্তু প্রস্থ ও উচ্চতা নেই, তাই রেখা।
৪.যে রেখার উপরিস্থিত বিন্দুগুলো একই বরাবরে থাকে, তাই সরলরেখা।
৫.যার কেবল দৈর্ঘ্য ও প্রস্থ আছে, তাই তল
৬.তলের প্রান্ত হলো রেখা।
৭.যে তলের সরলরেখাগুলো তার উপর সমভাবে থাকে, তাই সমতল।

ইউক্লিডিও স্বতঃসিদ্ধঃ
প্রকৃতপক্ষে, যেকোনো গাণিতিক বিশ্লেষণে গণিতের কিছু কিছু প্রাথমিক ধারণাকে স্বীকার করে নেওয়া হয়। ইউক্লিড এগুলোকে স্বতঃসিদ্ধ বলেছেন।
ইউক্লিড প্রদত্ত স্বতঃসিদ্ধগুলো নিম্নরূপঃ
১.যে সকল বস্তু একই বস্তুর সমান, সেগুলো পরস্পর সমান।
২.সমান সমান বস্তুর সাথে সমান বস্তু যোগ করা হলে যোগফল সমান।
৩.সমান সমান বস্তু থেকে সমান বস্তু বিয়োগ করা হলে বিয়োগফল সমান।
৪.যা পরস্পরের সাথে মিলে যায়, তা পরস্পর সমান।
৫.পূর্ণ তার অংশের চেয়ে বড়।

ইউক্লিডিও স্বীকার্যঃ
আধুনিক গণিত তথা জ্যামিতিতে প্রাথমিক ধারণা হিসাবে বিন্দু, রেখা এবং সমতলকে গ্রহণ করে এদের কোনো কোনো বৈশিষ্ট্যকে স্বীকার করে নেওয়া হয়। জ্যামিতির এইসব স্বীকৃত বৈশিষ্ট্যগুলোই স্বীকার্য হিসাবে পরিচিত। তবে বাস্তব ধারণা ও বিশ্লেষণের সাথে মিল রেখেই এইসব স্বীকার্যগুলো পরিপূর্ণরূপ লাভ করেছে।
ইউক্লিড প্রদত্ত স্বীকার্যগুলো নিম্নরূপঃ
১.একটি বিন্দু থেকে অন্য একটি বিন্দু পর্যন্ত একটি সরলরেখা আঁকা যায়।
২.খণ্ডিত রেখাকে যথেচ্ছভাবে বাড়নো যায়।
৩.যে কোনো কেন্দ্র ও যেকোনো ব্যাসার্ধ নিয়ে বৃত্ত আঁকা যায়।
৪.সকল সমকোণ পরস্পর সমান।
৫.একটি সরলরেখা অপর দুইটি সরলরেখাকে ছেদ করলে এবং ছেদকের একই পাশের অন্তঃস্থ কোণদ্বয়ের সমষ্টি দুই সমকোণের চেয়ে কম হলে, রেখা দুইটিকে যথেচ্ছভাবে বাড়ানো হলে যেদিকে কোণের সমষ্টি দুই সমকোণের চেয়ে কম, সেদিকে মিলিত হয়।

জ্যামিতিক রাশি ও ক্ষেত্রের সংঙ্গাঃ

জ্যামিতিক রাশি ও ক্ষেত্রের সংঙ্গা নিম্নরুপঃ
কোণঃ
কোণ কাকে বলে?
যদি দুইটি সরলরেখা পরস্পরের সাথে কোনো বিন্দুতে মিলিত হয়, তবে মিলন বিন্দুতে কোণ উৎপন্ন হয়। দুটি সরলরেখা তির্যকভাবে পরস্পরের সাথে মিলিত হলে মিলিত বিন্দুতে কোণ উৎপন্ন হয়।

সূক্ষ্মকোণ কাকে বলে?
এক সমকোণ (90 ডিগ্রী) অপেক্ষা ছোট কোণকে সূক্ষ্মকোণ বলে।

স্থূলকোণ কাকে বলে?
এক সমকোণ অপেক্ষা বড় বিন্তু দুই সমকোণ অপেক্ষা ছোট কোণকে সথূলকোণ বলে।

সমকোণ কাকে বলে?
একটি সরল রেখার উপর অন্য একটি লম্ব টানলে এবং লম্বের দু’পাশে অবস্থিত ভূমি সংলগ্ন কোণ দুটি সমান হলে, প্রতিটি কোণকে সমকোণ বলে। এক সমকোণ = 90 ডিগ্রী

প্রবৃদ্ধকোণ কাকে বলে?
দুই সমকোণ অপেক্ষা বড় কিন্তু চার সমকোণ অপেক্ষা ছোট কোণকে প্রবদ্ধ কোণ বলে। অর্থাৎ 360 > x > 180 হলে x একটি প্রবৃদ্ধ কোণ।

সরলকোণ কাকে বলে? 
দু’টি সরল রেখা পরস্পর বিপরীত দিকে গমন করলে রেখাটির দু’পাশে যে কোণ উৎপন্ন হয় তাকে সরলকোণ বলে। সরলকোণ দুই সমকোণের সমান বা 180 ডিগ্রী। 

বিপ্রতীপকোণ কাকে বলে?
দু’টি সরল রেখা পরস্পর ছেদ করলে যে চারটি কোণ উৎপন্ন হয় এদের একটিকে তার বিপরীত কোণের বিপ্রতীপ কোণ বলে।

সম্পূরককোণ কাকে বলে?
দু’টি কোণের সমষ্টি 180 ডিগ্রী বা দুই সমকোণ হলে একটিকে অপরটির সম্পূরক কোণ বলে

পূরককোণ কাকে বলে?
দু’টি কোণের সমষ্টি এক সমকোণ বা 90 ডিগ্রী হলে একটিকে অপরটির পূরক কোণ বলে।

অনুরূপকোণ কাকে বলে?
দু’টি সমান্তরাল সরল রেখাকে অপর একটি সরল রেখা ছেদ করলে ছেদকের একই পাশে সমান্তরাল রেখাদ্বয়ের সাথে যে কোণ উৎপন্ন হয় তকে অনুরূপ কোণ বলে। অনুরূপ কোণগুলো পরস্পর সমান হয়।

সন্নিহিতকোণ কাকে বলে?
যদি দু’টি কোণের একটি সাধারণ বাহু থাকে তবে একটি কোণের অপর কোণের সন্নিহিত কোণ বলে।

ত্রিভুজঃ
ত্রিভুজ কাকে বলে?
তিনটি সরলরেখা দ্বারা সীমাবদ্ধ ক্ষেত্রকে ত্রিভূজ বলে। 

সুক্ষ্মকোণীত্রিভূজ কাকে বলে?
যে ত্রিভূজের তিনটি কোণই এক সমকোণ(90 ডিগ্রী ) এর ছোট তাকে সূক্ষ্মকোণী ত্রিভূজ বলে।

স্থূলকোণীত্রিভূজ কাকে বলে?
যে ত্রিভূজের একটি কোণ সথূলকোণ বা এক সমকোণ অপেক্ষা বড় তাকে সথূলকোণী ত্রিভূজ বলে। কোন ত্রিভূজের একের অধিক সথূলকোণ থাকতে পারে না।

সমকোণী ত্রিভূজ কাকে বলে?
যে ত্রিভূজের একটি কোণ সমকোণ তাকে সমকোণী ত্রিভূজ বলে। কোন ত্রিভূজে একটির অধিক সমকোণ থাকতে পারে না। সমকোণী ত্রিভূজের সমকোণের বিপরীত বাহুকে অতিভূজ এবং সমকোণ সংলগ্ন বাহুদ্বয়ের একটিকে ভূমি এবং অপরটিকে লম্ব বলা হয়।

লম্বকেন্দ্র কাকে বলে? 
ত্রিভুজের তিনটি শীর্ষ থেকে বিপরীত বাহুগুলির উপর তিনটি লম্ব সমবিন্দুগামী, এবং বিন্দুটির নাম লম্বকেন্দ্র(orthocenter)। 

সমবাহু ত্রিভুজ কাকে বলে?
যে ত্রিভুজের তিনটি বাহুই সমান তাকে সমবাহু ত্রিভুজ বলে।

সমদ্বিবাহু ত্রিভুজ কাকে বলে?
যে ত্রিভুজের দুটি বাহু পরস্পর সমান এবং অপর বাহুটি অসমান তাকে সমদ্বিবাহু ত্রিভুজ বলে।

বিষমবাহু ত্রিভুজ কাকে বলে?
যে ত্রিভুজের তিনটি বাহুই পরস্পর অসমান তাকে বিষোমবাহু ত্রিভুজ বলে।

অতিভুজ কাকে বলে?
সমকোণী ত্রিভুজের সমকোণের বিপরীত বাহুর নাম অতিভুজ। পিথাগোরাসের বিখ্যাত উপপাদ্য অনুযায়ী সমকোণী ত্রিভুজের অতিভুজের বর্গ এর সমকোণ-সংলগ্ন দুই বাহুর বর্গের যোগফলের সমান।

অন্তঃস্থ কোণ কাকে বলে?
ত্রিভুজের অভ্যন্তরস্থ কোনগুলিকে অন্তঃস্থ কোণ বলে। ত্রিভুজের তিনটি অন্তঃস্থ কোণের সমষ্টি ১৮০°।

বহিঃস্থ কোণ কাকে বলে?
ত্রিভুজের বাহুগুলিকে বর্ধিত করলে যে কোণগুলি পাওয়া যায়, তাদেরকে বহিঃস্থ কোণ বলে। । যেকোন বহিঃস্থ কোণ এর অন্তঃস্থ বিপরীত কোণদ্বয়ের সমষ্টির সমান।

মধ্যমা কাকে বলে? 
ত্রিভুজের কোন শীর্ষবিন্দু থেকে বিপরীত বাহুর মধ্যবিন্দু পর্যন্ত আঁকা রেখাকে বলা হয় ত্রিভুজটির একটি মধ্যমা। ত্রিভুজের তিনটি মধ্যমা একই বিন্দুতে ছেদ করে এবং এটি প্রতিটি মধ্যমার শীর্ষবিন্দু থেকে দুই-তৃতীয়াংশ দূরত্বে অবস্থিত।

ত্রিভুজের উচ্চতা কাকে বলে?
ত্রিভুজের কোন শীর্ষবিন্দু থেকে বিপরীত বাহুর উপর অঙ্কিত লম্বকে ঐ ত্রিভুজের উচ্চতা বলে।

সর্বসম ত্রিভুজ কাকে বলে? 
দুইটি ত্রিভুজকে সর্বসম বলা হয় যদি এগুলি নিচের তিনটি শর্তের সেটের যেকোনটি পূরণ করেঃ

(১) একটি ত্রিভুজের এক বাহু ও দুইটি কোণ অন্যটির অনুরূপ বাহু ও দুইটি কোণের সমান;
(২) কোন একটি ত্রিভুজের দুই বাহু এবং এদের অন্তর্ভুক্ত কোণ অন্য ত্রিভুজটির দুই বাহু ও অন্তর্ভুক্ত কোণের সমান; অথবা
(৩) একটি ত্রিভুজের তিনটি বাহু অপর ত্রিভুজের তিন বাহুর সমান। যদি একই সমতলে অবস্থিত দুইটি ত্রিভুজকে নিখুঁতভাবে একটির উপর আরেকটিকে বসিয়ে দেয়া যায়, তবে তারা সরাসরি সর্বসম। আর যদি বসানোর আগে একটিকে উল্টে নিতে হয়, তবে ত্রিভুজ দুটি বিপরীতভাবে সর্বসম।

সদৃশ ত্রিভুজ কাকে বলে? 
যদি দুইটি ত্রিভুজের একটির সবগুলি কোণ অন্যটির সবগুলি কোণের সমান হয়, তবে তাদেরকে সদৃশ ত্রিভুজ বলা হয় এবং এদের অনুরূপ বাহুগুলি সমানুপাতিক হয়।

অন্তঃকেন্দ্র কাকে বলে?
ত্রিভুজের কোণত্রয়ের সমদ্বিখন্ডকগুলো সমবিন্দু । এ বিন্দুই ত্রিভুজের অন্তঃকেন্দ্র।

পরিকেন্দ্র কাকে বলে?
ত্রিভুজের বাহুত্রয়ের লম্বদ্বিখন্ডকত্রয় সমবিন্দু। এই বিন্দু ত্রিভুজের পরিকেন্দ্র।

ভরকেন্দ্র কাকে বলে?
ত্রিভুজের কোণ একটি শীর্ষবিন্দু এবং তার বিপরীত বাহুর মধ্যবিন্দুর সংযোজক সরলরেখাকে মধ্যমা বলে। ত্রিভুজের মধ্যমাত্রয় সমবিন্দু । এই বিন্দুকে ত্রিভুজের ভরকেন্দ্র বলে।

চতুর্ভুজঃ
চতুর্ভুজ কাকে বলে?
চারটি রেখাংশ দিয়ে সীমাবদ্ধ ক্ষেত্রকে চতুর্ভুজ বলে।

কর্ণ কাকে বলে?
চতুর্ভুজের বিপরীত শীর্ষ বিন্দুগুলোর দিয়ে তৈরি রেখাংশকে কর্ণ বলে। চতুর্ভুজের কর্ণদ্বয়ের সমষ্টি তার পরিসীমার চেয়ে কম।

সামান্তরিক কাকে বলে?
যে চতুর্ভুজের বিপরীত বাহুগুলো সমান ও সমান্তরাল এবং বিপরীত কোণগুলো সমান (কিন্তু কোণ গুলো সমকোন নয়) , তাকে সামান্তরিক বলে।

আয়তক্ষেত্র কাকে বলে?
যে চতুর্ভুজের বিপরীত বাহুগুলো সমান ও সমান্তরাল এবং প্রতিটি কোণ সমকোণ, তাকে আয়ত বলে।

বর্গক্ষেত্র কাকে বলে?
যে চতুর্ভুজের চারটি বাহুই পরস্পর সমান এবং কোণগুলো সমকোণ তাকে বর্গক্ষেত্র বলে।

রম্বস কাকে বলে? 
রম্বস এক ধরনের সামান্তরিক যার সবগুলি বাহু সমান কিন্তু কোণ গুলো সমকোন নয়

ট্রাপিজিয়াম কাকে বলে? 
যে চতুর্ভুজ এর দুইটি বাহু সমান্তরাল কিন্তু অসমান, তাকে ট্রাপিজিয়াম বলে।

সুষম বহুভুজ কাকে বলে?

যদি বহুভুজের সবগুলি বাহু ও কোণ সমান হয়, তবে সেটিকে সুষম বহুভুজ বলে।

বৃত্তঃ

বৃত্ত কাকে বলে?

একই সমতলে অবস্থিত একটি নির্দিষ্ট বিন্দু থেকে সমদুরবর্তী সকল বিন্দু দ্বারা গঠিত সুষম আবদ্ধ বক্রাকার চিত্রকে বৃত্ত বলে

কেন্দ্র কাকে বলে?

যে নির্দিষ্ট বিন্দু থেকে বৃত্তের পরিধির উপর সকল বিন্দুর দূরত্ব সমান সেই বিন্দুকে কেন্দ্র বলে।

ব্যাসার্ধ কাকে বলে?

বৃত্তের কেন্দ্র থেকে পরিধির উপর যেকোনো বিন্দুর দূরত্ব কে ব্যাসার্ধ বলে।

জ্যা কাকে বলে?

বৃত্তের পরিধির উপর যেই কোন দুটি বিন্দুর সংযোজক রেখাংশ কে জ্যা বলে।

ব্যাস কাকে বলে?

বৃত্তের কেন্দ্রগামী জ্যাকে ব্যাস বলে।

পরিধি কাকে বলে?

বৃত্তের সীমান্ত বরাবর দৈর্ঘ্যকে পরিধি বলে।

বৃত্তচাপ কাকে বলে? 

বৃত্তের যেকোনো দুটি বিন্দুর মধ্যে পরিধির অংশকে চাপ বলে।

অর্ধ-বৃত্তচাপ কাকে বলে?
যে বৃত্তচাপের দৈর্ঘ্য পরিধির অর্ধেক তাকে অর্ধবৃত্ত বলে।

বৃত্তাংশ কাকে বলে?

বৃত্তের একটি জ্যা ও একটি চাপ দ্বারা গঠিত অংশকে বৃত্তাংশ বলে।

বৃত্তকলা কাকে বলে?

বৃত্তের দুইটি ব্যাসার্ধ ও একটি চাপ দ্বারা গঠিত অঞ্চলকে বৃত্তকলা বলে।

বৃত্তস্থকোণ কাকে বলে?

বৃত্তের দুটি জ্যা পরস্পর কে বৃত্তের উপর কোন বিন্দুতে ছেদ করলে এদের মধ্যবর্তী কোণকে বৃত্তস্থ কোণ বা বৃত্তে অন্তর্লিখিত কোন বলে।

কেন্দ্রস্থ কোণ কাকে বলে?

একটি কোণের শীর্ষবিন্দু কোন বৃত্তের কেন্দ্রে অবস্থিত হলে কোণটিকে ঐ বৃত্তের একটি কেন্দ্রস্থ কোণ বলা হয়।

বৃত্তস্থ চতুর্ভুজ কাকে বলে?

যে চতুর্ভুজের চারটি শীর্ষবিন্দু বৃত্তের উপর অবস্থিত হয় সেই চতুর্ভুজকে বৃত্তস্থ চতুর্ভুজ বলে।

স্পর্শক কাকে বলে?

একটি বৃত্ত ও একটি সরলরেখার যদি একটি ও কেবল ছেদবিন্দু থাকে তবে সরলরেখাটিকে বৃত্তের স্পর্শক বলা হয়।

সাধারণ স্পর্শক কাকে বলে? 

একটি সরলরেখা যদি দুইটি বৃত্তের স্পর্শক হয় তবে উক্ত রেখাটিকে সাধারণ স্পর্শক বলা হয়।

পরিবৃত্ত কাকে বলে?

তিনটি শীর্ষবিন্দু যোগ করে যেমন একটিমাত্র ত্রিভুজ হয় তেমনি তিনটি বিন্দু (শীর্ষ)গামী বৃত্তও একটিই, এর নাম পরিবৃত্ত।

পরিকেন্দ্র কাকে বলে?

পরিবৃত্তের কেন্দ্র কে পরিকেন্দ্র।

কনিকঃ

কনিক কাকে বলে?

কার্তেসীয় সমতলে একটি নির্দিষ্ট বিন্দু ও একটি নির্দিষ্ট সরলরেখা থেকে যে সব বিন্দুর দূরত্বের অনুপাত একটি ধ্রুবক, তাদের সেই একটি সঞ্চারপথ এবং তাকে কনিক বলা হয় ।

উপবৃত্ত কাকে বলে?

উপবৃত্ত হলো কতকগুলো বিন্দুর সমন্বয়ে গঠিত এমন একটি সমতলীয় বদ্ধ বক্ররেখা যেন ঐ বক্ররেখার উপর অবস্থিত যে কোন বিন্দু হতে দুইটি নির্দিষ্ট বিন্দুর দুরত্বের সমষ্টি সব সময়ই একটি নির্দিষ্ট ধ্রূবক। প্রতিটি নির্দিষ্ট বিন্দুকে উপবৃত্তের ফোকাস বা উপকেন্দ্র বলে। যেহেতু এমন দুইটি নির্দিষ্ট বিন্দু রয়েছে, তাই উপবৃত্তের ফোকাস বা উপকেন্দ্র দুইটি। ফোকাস বিন্দু দুইটির মধ্যবর্তী দুরত্বকে ফোকাস দুরত্ব বলে। উপকেন্দ্র বিন্দু দুইটির সংযোজক রেখাংশের মধ্যবিন্দুই হলো উপবৃত্তের কেন্দ্র।

অধিবৃত্ত কাকে বলে? 

অধিবৃত্ত হলো কতকগুলো বিন্দুর সমন্বয়ে গঠিত এমন একটি সমতলীয় খোলা বক্ররেখা যেন ঐ বক্ররেখার উপর যেকোন বিন্দু হতে একটি নির্দিষ্ট বিন্দু এবং একটি নির্দিষ্ট রেখা উভয়েরই দুরত্ব সমান। নির্দিষ্ট বিন্দুটিকে বলা হয় অধিবৃত্তের উপকেন্দ্র বা ফোকাস এবং নির্দিষ্ট রেখাটিকে বলা হয় অধিবৃত্তের দ্বিকাক্ষ।

পরাবৃত্তঃ

পরাবৃত্ত কাকে বলে?

পরাবৃত্ত হলো কতকগুলো বিন্দুর সমন্বয়ে গঠিত এমন দুইটি সমতলীয় খোলা বক্ররেখা যেন ঐ বক্ররেখা দুইটির অভ্যন্তরস্থ দুইটি নির্দিষ্ট বিন্দু হতে প্রতিটি বক্ররেখার উপর অবস্থিত যেকোন একটি বিন্দুর দুরত্বের পার্থক্যের পরম মান সবসময়ই একটি নির্দিষ্ট ধ্রূবকের সমান। প্রতিটি নির্দিষ্ট বিন্দুকে ফোকাস বা উপকেন্দ্র বলে। যেহেতু এমন দুইটি নির্দিষ্ট বিন্দু রয়েছে, তাই পরাবৃত্তের উপকেন্দ্র দুইটি। উপকেন্দ্রদ্বয়ের সংযোজক রেখাংশের মধ্যবিন্দুকে পরাবৃত্তের কেন্দ্র বলে। দ্বিমাত্রিক জগতে পরাবৃত্ত হলো একই সমতলে অবস্থিত দুইটি প্রতিসাম্য বক্ররেখা বা একটি বক্ররেখা আরেকটির আয়না প্রতিচ্ছবি।

পরাবৃত্তের ফোকাস বা উপকেন্দ্র কাকে বলে? 

ফোকাস বা উপকেন্দ্র হলো পরাবৃত্ত বক্ররেখার অভ্যন্তরস্থ এমন দুইটি নির্দিষ্ট বিন্দু যাদের থেকে পরাবৃত্ত বক্ররেখা দুইটির যেকোন একটির উপর যেকোন বিন্দুর দুরত্বের পার্থক্যের পরম মান একটি নির্দিষ্ট ধ্রূবক।

সম্পর্কিত আর্টিকেল ;- দশমিক ভগ্নাংশ কাকে বলে? কত প্রকার ও কি কি?

পরাবৃত্তের কেন্দ্র কাকে বলে?

পরাবৃত্তের উপকেন্দ্র দুইটির সংযোজক রেখাংশের মধ্যবিন্দুকে পরাবৃত্তের কেন্দ্র বলে। অন্যভাবে বললে, পরাবৃত্তের বৃহৎ অক্ষ ও ক্ষুদ্র অক্ষের ছেদ বিন্দুকে কেন্দ্র বলে। তাছাড়া এই কেন্দ্র বিন্দুতে অক্ষদ্বয় পরস্পর সমকোণে মিলিত হয়।

পরাবৃত্তের বৃহৎ অক্ষ কাকে বলে?

বৃহৎ অক্ষ হলো উপকেন্দ্রদ্বয় দিয়ে অতিক্রমকারী সরলরেখা। পরাবৃত্তের বৃহৎ অক্ষ আবার প্রতিসাম্য রেখা বলে পরিচিত। বৃহৎ অক্ষের দৈর্ঘ্য হলো 2a. সুতরাং, অর্ধ বৃহৎ অক্ষের দৈর্ঘ্য হলো a.

পরাবৃত্তের শীর্ষ কাকে বলে?

বৃহৎ অক্ষ পরাবৃত্তকে যে বিন্দুতে ছেদ করে তাকে শীর্ষ বিন্দু বলে। অন্যভাবে বললে, উপকেন্দ্রদ্বয়ের সংযোজক রেখাংশ পরাবৃত্ত বক্ররেখা দুইটিকে যে দুইটি বিন্দুতে ছেদ করে তাদেরকে শীর্ষ বিন্দু বলে। কেন্দ্র থেকে যেকোন শীর্ষ বিন্দুর দুরত্ব $a$ যা অর্ধ বৃহৎ অক্ষের দুরত্বের সমান।

পরাবৃত্তের অসীম তট কাকে বলে?

অসীম তট হলো কেন্দ্রগামী এমন একটি সরলরেখা যা পরাবৃত্তের বক্ররেখাকে কখনও ছেদ করবে না।

পরাবৃত্তের ফোকাস দুরত্ব বা উপকেন্দ্রিক দুরত্ব কাকে বলে? 

কেন্দ্র থেকে যেকোন ফোকাস বা উপকেন্দ্রের দুরত্বকে ফোকাস দুরত্ব বা উপকেন্দ্রিক দুরত্ব বলে।

আরো পড়ুন ;- ব্যাকরণ কাকে বলে? ব্যকরণ কত প্রকার ও কি?

পরাবৃত্তের উপকেন্দ্রিকতা কাকে বলে? 

ফোকাস দুরত্ব ও অর্ধ বৃহৎ অক্ষের দৈর্ঘ্যের অনুপাতকে উপকেন্দ্রিকতা বলে। এটিকে e দ্বারা সূচিত করা হয়। যদি পরাবৃত্তের ফোকাস দুরত্ব c এবং অর্ধ বৃহৎ অক্ষের দৈর্ঘ্য a হয়, তাহলে উপকেন্দ্রিকতা e = ca পরাবৃত্তের উপকেন্দ্রিকতা সবসময় এক অপেক্ষা বড় অর্থাৎ e > 1.

পরাবৃত্তের দ্বিকাক্ষ বা নিয়ামক কাকে বলে?
দ্বিকাক্ষ বা নিয়ামক হলো কেন্দ্র হতে a2c একক দুরত্বে অবস্থিত বৃহৎ অক্ষের উপর লম্ব একটি সরলরেখা যেখানে a ও c হলো যথাক্রমে অর্ধ বৃহৎ অক্ষের দৈর্ঘ্য ও ফোকাস দুরত্ব। একটি পরাবৃত্তের এরূপ দুইটি দ্বিকাক্ষ থাকে।

পরাবৃত্তের উপকেন্দ্রিক লম্ব কাকে বলে?

বৃহৎ অক্ষের উপর লম্ব এবং যেকোন উপকেন্দ্রগামী জ্যাকে উপকেন্দ্রিক লম্ব বলে। অন্যভাবে বলা যায়, উপকেন্দ্রিক লম্ব হলো বৃহৎ অক্ষের উপর লম্ব এবং উপকেন্দ্রগামী এমন একটি রেখাংশ যার প্রান্তবিন্দুদ্বয় পরাবৃত্তের বক্ররেখার উপর অবস্থিত। এটি উপকেন্দ্রগামী একটি বিশেষ জ্যা। আবার এটি উপকেন্দ্রগামী একটি অনন্য জ্যা যা বৃহৎ অক্ষ বা প্রতিসাম্য অক্ষ দ্বারা সমদ্বিখণ্ডিত হয়।

গোলক কাকে বলে?

দুইটি পরস্পর বিপরীত রশ্মি তাদের সাধারণ প্রান্ত বিন্দুতে যে কোণ উৎপন্ন করে, তাকে সরল কোণ বলে ।

আরো জানুন ;- শব্দ কাকে বলে? কত প্রকার ও কি কি?

ঘনবস্তু কাকে বলে?

তিন জোড়া সমান্তরাল আয়তাকার সমতল বা পৃষ্ট দ্বারা আবদ্ধ ঘনবস্তুকে  ঘনবস্তু বলে।

ঘনক কাকে বলে?

আয়তাকার ঘনবস্তুর দৈর্ঘ্য, প্রস্থ ও উচ্চতা সমান হলে, তাকে ঘনক বলে ।

কোণক কাকে বলে?

কোন সমকোণী ত্রিভুজে সমকোণ সংলগ্ন যে কোন একটি বাহুকে স্থির রেখে ঐ বাহুর চতুর্দিকে ত্রিভুজটিকে ঘুরালে যে ঘনবস্তু উৎপন্ন হয় তাকে সমবৃত্তভুমিক কোণক বলে 

সিলিন্ডার বা বেলন কাকে বলে?

একটি আয়তক্ষেত্রের যে কোন একটি বাহুকে স্থির রেখে ঐ বাহুর চতুর্দিকে আয়তক্ষেত্রটিকে ঘুরালে যে ঘনবস্তু উৎপন্ন হয় তাকে সমবৃত্তভুমিক বেলন বলে ।

সম্পর্কিত আর্টিকেল ;- Letter কাকে বলে? কত প্রকার ও কি কি?

সর্বশেষ আপডেট

• From Village Dreams to Digital Design: The Inspiring Journey of Abu Shaid
• বাঁশ-দড়ি বেয়ে মসজিদে যান ১১৬ বছর বয়সী অন্ধ মুয়াজ্জিন
• সমুদ্র সৈকত নিয়ে ক্যাপশন | কক্সবাজার সমুদ্র সৈকত নিয়ে স্ট্যাটাস
• ব্যক্তিত্ব নিয়ে উক্তি ও ক্যাপশন | ব্যক্তিত্ব নিয়ে স্ট্যাটাস, কিছু কথা
• 250+ স্বামীকে নিয়ে ভালোবাসার স্ট্যাটাস, উক্তি ও ক্যাপশন