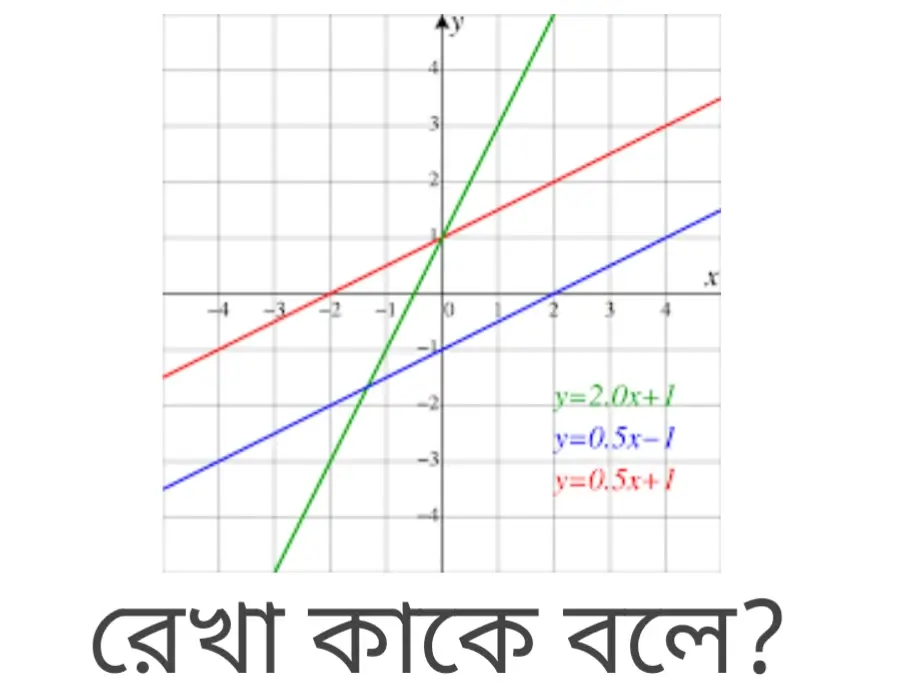
যার দৈর্ঘ্য আছে কিন্তু , প্রস্থ ও বেধ বা উচ্চতা নেই তাকে রেখা বলে। রেখার কোন প্রান্ত বিন্দু নেই,বতাই রেখাকে ইচ্ছামত উভয় দিকে বাড়ানো যায়।
রেখা কত প্রকার ও কি কি?
রেখা দুই প্রকার। যথা: সরলরবখা এবং বক্ররেখা।
১. সরল রেখা: যদি কোন বিন্দু সরল পথে চলে দুই দিকেই অসীম পর্যন্ত বিস্তৃত হয়, তবে তাকে সরলরেখা বলে।
২. বক্র রেখা: যদি কোন বিন্দু আঁকা বাঁকা পথে চলে দুই দিকেই অসীম পর্যন্ত বিস্তৃত হয়, তবে তাকে বক্ররেখা বলে।
বিন্দু
১। রেখার কোন প্রন্তবিন্দু নেই। ২। দুইট বিন্দুর মধ্যে দিয়ে একটি এবং কেবলমাত্র সরল রেখা আঁকা যায়। ৩।দুই বিন্দুর মধ্যে সরলরেখার দূরত্বই ক্ষুদ্রতম। ৪। যেসব বিন্দু একই সরলরেখায় অবস্থান করে, তাদেরকে সমরেখ বিন্দু বলে। ৫। দুটি সরলরেখা একটি এবং কেবল একটি বিন্দুতে ছেদ করতে পারে।
রেখার বৈশিষ্ট্যঃ
- ১. বিন্দু যে পথে যাই তাই-ই রেখা।
- ২. বিন্দু অনির্দিষ্ট স্থান থেকে আসে এবং পথ চলতে শুরু করে কিন্তু কখনো থামে না তাই এর কোন শেষ নেই।
- ৩. রেখার শুরু বা শেষ নেই।
- ৪. খাতায় বা কোথাও রেখা আকতে গেলে যেখান থেকে আকা শুরু করতে হয় সেখানে রেখার উপর তীর চিহ্ন দিতে হয় যাতে এটা বোঝা যায় যে এর আগেও আরো রেখা আছে।
- ৫. খাতায় বা কোথাও রেখা আকতে গেলে যেখানে রেখা আকা শেষ করতে হয় সেখানে রেখার উপর তীর চিহ্ন দিতে হয় যাতে এটা বোঝা যায় যে এর পরেও আরো রেখা আছে।
- ৬. রেখার কোন শুরু বা শেষ নেই তাই এর কোন প্রান্ত বা শেষ বিন্দু নেই।
- ৭. রেখা সোজা বা আঁকাবাঁকা যে কোন রকমি হতে পারে।
- ৮. রেখা থেকে রশ্মি এবং রেখাংশের উৎপত্তি বা সৃষ্টি হয়।
- ৯. ত্রিভুজ, চতুর্ভুজ বা বহুভুজ আঁকতে সরলরেখার প্রয়োজন হয়।
- ১০. রেখা দুই প্রকার হলেও কোথাও রেখার কথা উল্লেখ থাকলে সরলরেখা ধরা হয়।
- ১১. একটি বিন্দু অপর কোন বিন্দুকে কেন্দ্র করে বিন্দুটির চার পাশে সমান দুরত্ব রেখে একবার ঘুরে যে বাকা পথ বা রেখা তৈরি করে তাকে বৃত্তবলে।
- ১২. রেখার কোন প্রস্থ নেই।
- ১৩. রেখার দৈর্ঘ্য আছে কিন্তু নির্দিষ্ট কোন দৈর্ঘ্য নেই।
- ১৪. সরলরেখা কখনো নিজেকে ছেদ করতে পারে না।
- ১৫. বক্ররেখা নিজেকে যত ইচ্ছা ছেদ করতে পারে।
- ১৬. কোনো সরলরেখার উপর কোনো এক বিন্দুতে যে কোণ উৎপন্ন হয় তা দুই সমকোণ বা এক সরলকোণ বা ১৮০⁰ এর সমান।
আরো পড়ুন ;- জ্যামিতি কাকে বলে ? কত প্রকার ও কি কি?
সরলরেখার সমীকরণঃ
সরল রেখার সমীকরণ নির্ণয় করা যায়। বিন্দু, ঢাল, অক্ষদ্বয়ের ছেদক অংশ ইত্যাদির উপর নির্ভর করে সরলরেখার সমীকরণ গঠন করা যায়। সাধারণত যেসব নুন্যতম তথ্যের উপর ভিত্তি করে সরল রেখার সমীকরণ গঠন করা যায় তা নিচে দেওয়া হলো।
ঢাল ও একটি নির্দিষ্ট বিন্দু দিয়ে যায়
ঢাল ও যেকোন অক্ষের ছেদক
দুইটি নির্দিষ্ট বিন্দু দিয়ে গমনকারী
অক্ষদ্বয়ের ছেদকাংশ
ঢাল ও একটি নির্দিষ্ট বিন্দু দিয়ে গমনকারী সরলরেখার সমীকরণ এর সূত্র উদ্ভাবন
প্রথম পদ্বতি
P(x1,y1) এবং Q(x2,y2) বিন্দুগামী সরলরেখার ঢাল
m =
y2 – y1
x2 – x1
যেখানে x1 ≠ x2;
এখন P(x1,y1) যদি একটি নির্দিষ্ট বিন্দু এবং Q একটি চলক বিন্দু যেখানে Q(x,y) হয় অর্থাৎ, Q(x2,y2) = Q(x,y) হয়, তাহলে ঢাল দাঁড়ায়,
m =
y2 – y1
x2 – x1
বা, m =
y – y1
x – x1
∴ y – y1 = m(x – x1)
এটিই নির্ণেয় সরলরেখার সমীকরণ।
যেখানে x ≠ x1; কারণ x = x1 হলে তখন আর এটি সরলরেখা থাকে না; এটি তখন একটি বিন্দু হয়ে যায়।
দ্বিতীয় পদ্বতি
আবার (x1,y1) এবং (x2,y2) বিন্দুদ্বয় দিয়ে অতিক্রান্ত সরলরেখার ঢাল
m =
y2 – y1
x2 – x1
যেখানে x1 ≠ x2; এবং সরলরেখার সমীকরণটি
y – y1
y2 – y1-
x – x1
x2 – x1
বা,
y – y1
x – x1
=
y2 – y1
x2 – x1
বা,
y – y1
x – x1
= m
∴ y – y1 = m(x – x1)
কিছু বক্ররেখার নাম নিম্নে দেওয়া হল
খোলা বক্ররেখা (open curve)
বদ্ধ বক্ররেখা(closed curve)
সাধারণ(general curve)
পরাবৃত্তাকার বক্ররেখা(hyperbolic curve)
বর্গমূল বক্ররেখা(square root curve)
লগারিদমিক বক্ররেখা(log curve)
যৌগিক বক্ররেখা(compound curve)
উল্টো বক্ররেখা(reverse curve)
প্যাঁচানো বক্ররেখা(spiral curve)
ঘন বক্ররেখা(cubic curve)
তুরীয় বক্ররেখা(transcendental curve)
অধিবৃত্তাকার বক্ররেখা(parabolic curve)
বহুপদী বক্ররেখা(polynomial curve)
অনুভূমিক বক্ররেখা(horizontal curve)
সরল বক্ররেখা(simple curve)
বীজগাণিতিক বক্ররেখা(algebraic curve)
দ্বিঘাত বক্ররেখা(quadratic curve)ইহাই মূলত বক্ররেখার নাম হয়ে থাকে।
সম্পর্কিত আর্টিকেল ;- চতুর্ভুজ কাকে বলে? চতুর্ভুজ কত প্রকার ও কি কি?
সর্বশেষ আপডেট
- From Village Dreams to Digital Design: The Inspiring Journey of Abu Shaid
- বাঁশ-দড়ি বেয়ে মসজিদে যান ১১৬ বছর বয়সী অন্ধ মুয়াজ্জিন
- সমুদ্র সৈকত নিয়ে ক্যাপশন | কক্সবাজার সমুদ্র সৈকত নিয়ে স্ট্যাটাস
- ব্যক্তিত্ব নিয়ে উক্তি ও ক্যাপশন | ব্যক্তিত্ব নিয়ে স্ট্যাটাস, কিছু কথা
- 250+ স্বামীকে নিয়ে ভালোবাসার স্ট্যাটাস, উক্তি ও ক্যাপশন