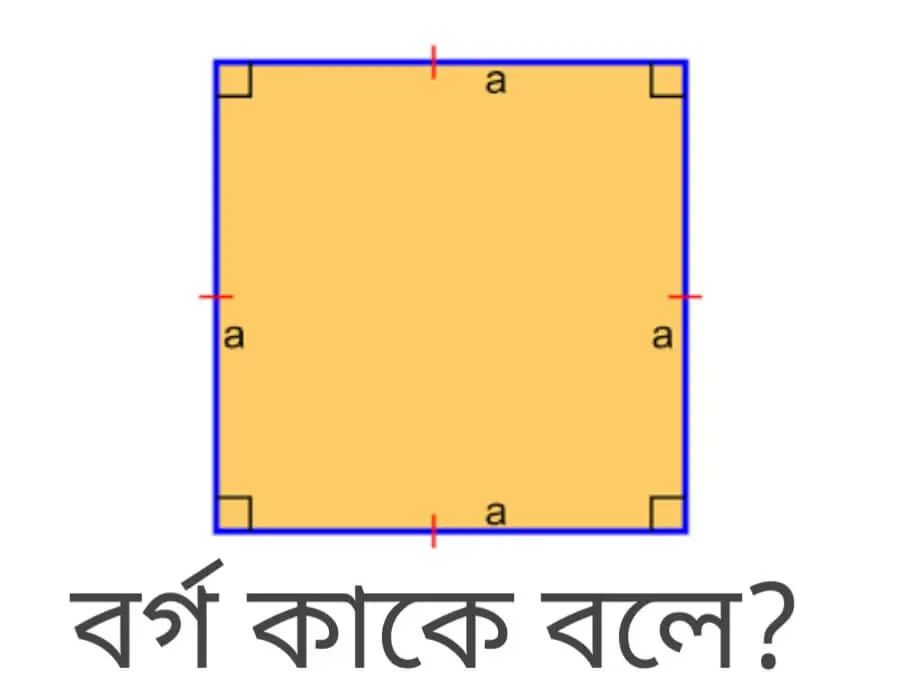
যে চতুর্ভুজের চারটি বাহুই পরস্পর সমান ও সমান্তরাল এবং প্রক্যেক কোণগুলো সমকোণ বা ৯০ ডিগ্রি তাকে বর্গ বলে। বর্গক্ষেত্রের কর্ণ বর্গক্ষেত্রটিকে দুইটি সর্বসম ত্রিভুজে বিভক্ত করে এবং এই ত্রিভুজ দুইটির প্রতেকেই সমকোণী ত্রিভুজ। বর্গক্ষেত্র একটি বিশেষ ধরণের আয়তক্ষেত্র, যে আয়তক্ষেত্রের চারটি বাহু পরস্পর সমান।
বর্গক্ষেত্রের পরিধি, তির্যক এবং ক্ষেত্রফল
বর্গক্ষেত্রের বৈশিষ্ট্যগুলি জানার সূত্রগুলি নিম্নরূপ:
ঘের (P): a যদি বর্গক্ষেত্রের পার্শ্ব দৈর্ঘ্য হয় (উপরের গ্রাফে দেখা যায়), ঘের হবে: P = 4 * a
তির্যক: আমাদের অবশ্যই মনে রাখতে হবে যে কর্ণগুলি বর্গকে দুটি সমান ত্রিভুজে ভাগ করে যা সমদ্বিবাহু সমকোণী ত্রিভুজ। অর্থাৎ, তারা 90º এর সমকোণ এবং 90º এর চেয়ে ছোট দুটি কোণ দ্বারা গঠিত। সমকোণ দুটি বাহুর মিলনের দ্বারা গঠিত হয় যাকে পা বলা হয়। এদিকে, ত্রিভুজের যে বাহুটি সমকোণের বিপরীতে থাকে তাকে কর্ণ বলা হয়। সুতরাং, যদি আমরা নীচের চিত্রটিকে একটি রেফারেন্স হিসাবে গ্রহণ করি, A, B এবং D (ছায়াযুক্ত এলাকা) শীর্ষবিন্দু দ্বারা গঠিত ত্রিভুজটি, কর্ণটি হবে পার্শ্ব DB, যেখানে পাগুলি AB এবং AD।
পাইথাগোরিয়ান উপপাদ্য আমাদের বলে যে আমরা যদি পাগুলিকে বর্গ করি এবং সেগুলি যোগ করি, তাহলে আমরা কর্ণের বর্গক্ষেত্র পাব, যেমনটি আমরা নিম্নলিখিত সূত্রে দেখতে পাচ্ছি (যেখানে d হল তির্যকের দৈর্ঘ্য এবং a হল বর্গক্ষেত্রের বাহুর দৈর্ঘ্য)।
ক্ষেত্রফলঃ ক্ষেত্রফলটি উচ্চতা দ্বারা ভিত্তিকে গুণ করে গণনা করা হয়, যা বর্গক্ষেত্রের ক্ষেত্রে একই পরিমাপ করে এবং পাশের দৈর্ঘ্যের সমান (a):তির্যকের দৈর্ঘ্যের একটি ফাংশন হিসাবে ক্ষেত্রটি খুঁজে পেতে, আমরা a কে d দ্বারা প্রতিস্থাপন করি , এটি বিবেচনায় নিয়ে।
বর্গক্ষেত্রের বৈশিষ্ট্যঃ
১। বর্গক্ষেত্রের সকল বাহু সমান হয়।
২। বর্গক্ষেত্রের প্রত্যেকটি কোন সমকোন হয় অর্থাৎ প্রত্যের কোনের পরিমান ৯০ ডিগ্রি।
৩। বর্গক্ষেত্রের কর্ণদ্বয় পরস্পর সমান হয়।
৪। বর্গক্ষেত্রের কর্ণদ্বয় পরস্পরকে সমকোনে সমদ্বিখন্ডিত করে।
বর্গক্ষেত্রের পরিসীমাঃ
বর্গক্ষেত্রের বাহুগুলোর সমষ্টিকে বর্গক্ষেত্রের পরিসীমা বলে। সুতরাং, বর্গক্ষেত্রের পরিসীমা বলতে এর চতুর্দিকের দৈর্ঘ্যকে বুঝায়। আবার বর্গক্ষেত্রের চারটি বাহুর দৈর্ঘ্য পরস্পর সমান, তাই এর একটি বাহুর দৈর্ঘ্যেকে চার দ্বারা গুণ করলে পরিসীমা পাওয়া যায়।
বর্গক্ষেত্রের পরিসীমা নির্ণয়ের সূত্র
মনেকরি ABCD বর্গক্ষেত্রের বাহুর দৈর্ঘ্য AB = BC = CD = AD = a এবং পরিসীমা P.
সুতরাং বর্গক্ষেত্রের পরিসীমা নির্ণয়ের সূত্র হবে,
P = (AB + BC + CD + AD) একক
বা, P = (a + a + a + a) একক
∴ P = 4a একক
সুতরাং, বর্গক্ষেত্রের পরিসীমা = 4×a একক
বর্গক্ষেত্রের বাহুর দৈর্ঘ্য a এবং পরিসীমা P হলে,
P = 4a একক
বর্গক্ষেত্রের কর্ণঃ
বর্গক্ষেত্রের বিপরীত শীর্ষ বিন্দু দুইটির সংযোজক রেখাংশকে বর্গক্ষেত্রের কর্ণ বলে। আর এই রেখাংশের দৈর্ঘ্যকে বর্গক্ষেত্রের কর্ণের দৈর্ঘ্য বলে। বর্গক্ষেত্রের যেকোন কর্ণ বর্গক্ষেত্রটিকে দুইটি সর্বসম ত্রিভুজে বিভক্ত করে। আবার এই ত্রিভুজ দুইটির প্রত্যেকটিই সমকোণী ত্রিভুজ এবং প্রত্যেকটি ত্রিভুজের ক্ষেত্রফল বর্গক্ষেত্রটির ক্ষেত্রফলের অর্ধেক। বর্গক্ষেত্রের কর্ণ দুইটির দৈর্ঘ্য পরস্পর সমান। এছাড়া, বর্গক্ষেত্রের একটি কর্ণ অপর কর্ণকে সমকোণে সমদ্বিখণ্ডিত করে।
বর্গক্ষেত্রের কর্ণের দৈর্ঘ্য নির্ণয়ের সূত্রঃ
মনেকরি, একটি বর্গক্ষেত্রের বাহুর দৈর্ঘ্য a এবং কর্ণ d. আবার a, a এবং d বাহু তিনটি দ্বারা যে ত্রিভুজ গঠিত হয় তা একটি সমকোণী ত্রিভুজ যেখানে ত্রিভুজটির অতিভুজ d এবং ভুমি ও লম্ব উভয়ই a ও a. সুতরাং, পিথাগোরাসের উপপাদ্য অনুসারে
d2 = a2 + a2
বা, d2 = ২a2
বা, d = √২a2
বা, d = a√২
বর্গক্ষেত্রের ক্ষেত্রফলঃ
বর্গক্ষেত্রের একটি বাহুর দৈর্ঘ্যকে বর্গ করলে বর্গক্ষেত্রের ক্ষেত্রফল পাওয়া যায়। বর্গক্ষেত্রের ক্ষেত্রফল বলতে বুঝায় বর্গক্ষেত্রটি দ্বারা কতটুকু জায়গা আবদ্ধ অর্থাৎ সমতলের কতটুকু জায়গা এই বর্গক্ষেত্রটি দখল করে আছে। ক্ষেত্রফল দ্বিমাত্রিক জ্যামিতির অন্তর্গত। এতএব বর্গক্ষেত্রের ক্ষেত্রফল দৈর্ঘ্য ও প্রস্থ দ্বারা গঠিত। তাই স্মরণ রাখা দরকার – ক্ষেত্রফল হলো সমতলের জায়গা মাত্র। তাই ক্ষেত্রফল পরিমাপে উচ্চতার সংশ্লিষ্টতা নেই।
বর্গক্ষেত্রের ক্ষেত্রফল নির্ণয়ের সূত্র
আয়তক্ষেত্রের দৈর্ঘ্যকে প্রস্থ দ্বারা গুণ করলে আয়তক্ষেত্রের ক্ষেত্রফল পাওয়া যায়। যেহেতু সব বর্গক্ষেত্রই এক একটি আয়তক্ষেত্র, তাই এর বাহুর দৈর্ঘ্যকে আরেক বাহুর দৈর্ঘ্য দ্বারা গুণ করলে ক্ষেত্রফল পাওয়া যায়।
সুতরাং বর্গক্ষেত্রের ক্ষেত্রফল= (দৈর্ঘ্য × দৈর্ঘ্য) বর্গএকক
একটি বর্গক্ষেত্রের বাহুর দৈর্ঘ্য a এবং ক্ষেত্রফল A হলে,
A = a × a বর্গএকক
∴ A = a2 বর্গএকক
বর্গক্ষেত্রের বাহুর দৈর্ঘ্য a এবং ক্ষেত্রফল A হলে,
A = a2 বর্গএকক
আয়ত এবং বর্গেরপার্থক্যঃ
আয়ত:
চতুর্ভুজের কোণগুলো সমকোণ বা ৯০০ হলে তাকে আয়ত বলে। চতুর্ভুজের বিপরীত বাহুগুলো পরস্পর সমান ও সমান্তরাল এবং প্রত্যেকটি অন্তঃস্থ কোণ সমকোণ বা ৯০ হলে তাকে আয়ত বলে। আয়তের সংজ্ঞা থেকে দেখা যাচ্ছে যে, আয়তের দুই জোড়া বিপরীত বাহু পরস্পর সমান ও সমান্তরাল। বিধায়, আয়ত একটি সামান্তরিক। কারণ সামান্তরিকের বিপরীত বাহুগুলো পরস্পর সমান ও সমান্তরাল।
বর্গ:
চতুর্ভুজের চারটি বাহু ও চারটি কোণ পরস্পর সমান হলে তাকে বর্গ বলে। বর্গ একটি সুষম ও সমকোণী চতুর্ভুজ। বর্গ দ্বারা আবদ্ধ ক্ষেত্রকে বর্গক্ষেত্র বলে। মূলতঃ বর্গক্ষেত্র দ্বারা বর্গের ক্ষেত্রফলকে বুঝায়। বর্গক্ষেত্র একটি সমবাহু চতুর্ভুজ; কারণ এর চারটি বাহু পরস্পর সমান। আবার এটি একটি সমকোণী চতুর্ভুজ; কারণ এর সবগুলো কোণ পরস্পর সমান এবং প্রত্যেকটি কোণের পরিমাপ সমকোণ বা ৯০।
বর্গক্ষেত্রের কর্ণ বর্গক্ষেত্রটিকে দুইটি সর্বসম ত্রিভুজে বিভক্ত করে এবং এই ত্রিভুজ দুইটির প্রতেকেই সমকোণী ত্রিভুজ। বর্গক্ষেত্র একটি বিশেষ ধরণের আয়তক্ষেত্র, যে আয়তক্ষে
চতুর্ভুজের কোণগুলো সমকোণ বা ৯০০ হলে তাকে আয়ত বলে। চতুর্ভুজের বিপরীত বাহুগুলো পরস্পর সমান ও সমান্তরাল। অন্যদিকে আয়ত ও বর্গের মধ্যে পার্থক্য নিম্নরূপ-
১। চতুর্ভুজের কোণগুলো সমকোণ বা ৯০০ হলে তাকে আয়ত বলে। চতুর্ভুজের বিপরীত বাহুগুলো পরস্পর সমান ও সমান্তরাল এবং প্রত্যেকটি অন্তঃস্থ কোণ সমকোণ বা ৯০ হলে তাকে আয়ত বলে। অন্যদিকে চতুর্ভুজের চারটি বাহু ও চারটি কোণ পরস্পর সমান হলে তাকে বর্গ বলে।
২। আয়তের বিপরীত বাহুগুলো পরস্পর সমান। অন্যদিকে বর্গের চারটি বাহু সমান।
৩। আয়তের বিপরীত বাহুগুলো পরস্পর সমান্তরাল। অন্যদিকে বর্গের দুটি সন্নিহিত বাহু সমান।
৪। আয়তের চারটি কোণই সমকোণ। অন্যদিকে বর্গের প্রতিটি কোণ সমকোণ।
৫। আয়তের চারটি কোণের সমষ্টি চার সমকোণ বা ৩৬০ ডিগ্রি। অন্যদিকে বর্গক্ষেত্রের প্রত্যেকটি কোন সমকোন হয় অর্থাৎ প্রত্যের কোনের পরিমান ৯০ ডিগ্রি।
সর্বশেষ আপডেট
- From Village Dreams to Digital Design: The Inspiring Journey of Abu Shaid
- বাঁশ-দড়ি বেয়ে মসজিদে যান ১১৬ বছর বয়সী অন্ধ মুয়াজ্জিন
- সমুদ্র সৈকত নিয়ে ক্যাপশন | কক্সবাজার সমুদ্র সৈকত নিয়ে স্ট্যাটাস
- ব্যক্তিত্ব নিয়ে উক্তি ও ক্যাপশন | ব্যক্তিত্ব নিয়ে স্ট্যাটাস, কিছু কথা
- 250+ স্বামীকে নিয়ে ভালোবাসার স্ট্যাটাস, উক্তি ও ক্যাপশন